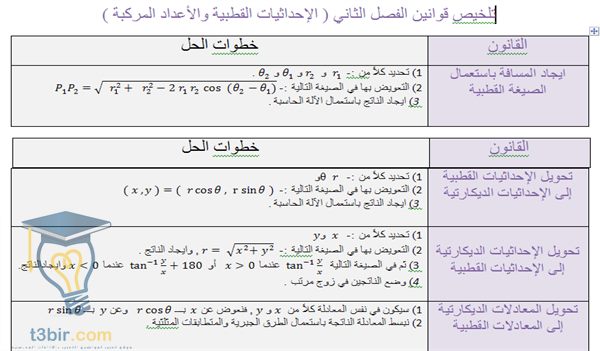
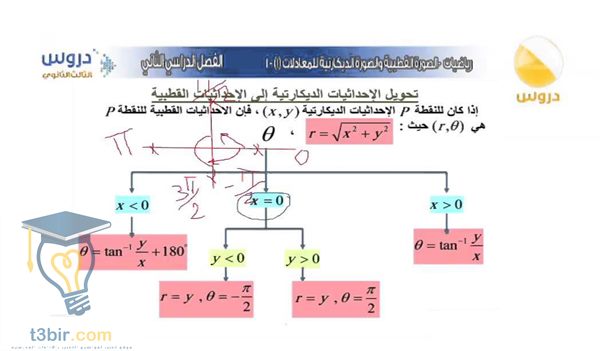
بحث عن الاحداثيات القطبية
بحث عن الاحداثيات القطبية والاعداد المركبةفما لاشك فيه ان الاحداثيات هي أرقام تقوم بوصف المكان النسبي النقاط في المستوى أو الفضاء الهندسي و على سبيل المثال ” أن الارتفاع بالنسبة لسطح البحر هي احداثيه ” فإنها تفيد في تحديد الارتفاع النسبي نقطة من الأرض .
إن نظام الاحداثيات فى المستوى أو الفضاء الهندسي هو عبارة عن نظام يقوم بإعطاء زوج من الأرقام أو أكثر لكل نقطة في الفضاء أو المستوى الهندسي للقيام بتحديد احداثياتها بدقة ؛ وهي لغة رياضية يتم استخدامها لوصف الأجسام الرياضية و تحليلها فإن عرفت احداثيات مجموعة من النقط فيمكنك الحصول على العلاقة بين النقط و تخصصها .
ان الجملة الاحداثية هي عبارة عن مخطط تحديد موضع نقطة في فضاء معين من خلال كميات عددية محددة عن طريق الاعتماد على بعض الأطر المرجعية و ان هذه الكليات هي إحداثيات النقطة ؛ و أن لكل مجموعة من الإحداثيات يوجد نقطة واحدة فقط مهما كان الجمل الاحداثية .
الاحداثيات القطبية
إن النظام الاحداثي القطبي هو عبارة عن نظام إحداثيات ثنائي الأبعاد ؛ حيث يقوم بتحديد مكان كل نقطة فى المستوى من خلال المسافة التي تفصل النقطة عن مركز ما و بزاوية تكون بين المستقيم المار من المركز و النقطة نفسها ؛ و هو عبارة عن مجموعة من المتغيرات تمكنك من معرفة مكان نقطة ما فى مستوى ثنائي الأبعاد .
و على العكس من الاحداثيات الديكارتية التى تقوم باستعمال نظام الاحداثي الكروى او القطبي نصف القطر و زاوية المسقط على الدائرة الاستوائية ؛ و زاوية المسقط على الدائرة القطبية .
حيث انه يتم تحديد كل نقطة داخل المستوى بالكامل بزاوية او اكثر و بعد ؛ و ان هذا النظام يكون مفيد بشكل خاص فى الحالات التى يوجد فيها انه من السهل التعبير عن العلاقة من خلال نقطتين من حيث المسافة و الزاوية ؛ مثلما هو الحال فى البندول .
و فى هذه الحالة سوف يشمل نظام الإحداثيات الديكارتية و هو الأكثر استخداما صيغ مثلثية للتعبير عن تلك العلاقة ؛ وبما انه نظام ثنائي الأبعاد فسوف يتم تحديد كل نقطة بواسطة إحداثيات قطبية توصف ب ” متجه شعاعي و زاوية ” .
*اقرا ايضا بحث عن ضرب العبارات النسبية وقسمتها
تاريخ الإحداثيات القطبية
فى منتصف القرن السابع عشر قام كل من ( بونافنتورا كافاليري ) و ( سانت فنست ) بتقديم هذا المصطلح بشكل مستقل ؛ و كتب سانت فنسنت في عام 1625 م عن هذا الامر بالتفصيل و قد تم نشر أعماله في عام 1647 م ؛ فى حين أن ما قام ( بونافنتورا كافاليري ) بكتابته لم ينشر قبل عام 1635 م و فى عام 1653 قد تم انشاء النسخة المصححة الاولى.
النظام الإحداثي بشكل عام
فى الرياضيات النظام الإحداثي هو عبارة عن نظام من خلاله من الممكن تعيين عدد ما من الأعداد و الكميات لكل نقطة موجودة فى الفضاء ذو بعد ؛ وبشكل عام فإن تلك الكميات تكون أعداد حقيقية و لكن فى بعض الحالات من الممكن أن تكون هذه الاعداد اعداد عقدية.
نظام الإحداثيات ثلاثي الابعاد
إن نظام الإحداثيات ثلاثي الابعاد يقوم بتوفير الأبعاد الفيزيائية الثلاث ” الطول ؛ و العرض ؛ و الارتفاع ” ؛ و ان الاحداثيات فى النظام الثلاثي الابعاد تكون على شكل ” س ؛ ص ؛ ز ” و على سبيل المثال ( فإنه يتم تصوير نقطتين فى نظام الصورة ؛ النقطة أ ” 5 ؛ 0 ؛ 3 ” و النقطة ب ” -5 ؛ -7 ؛ 5 ” ) .
من الممكن استنتاج احداثيات كل من س ؛ ص ؛ ز من الأبعاد على مستوى ص ؛ ز و المستوى س ؛ ص ؛ و يتم تقسيم محاور النظام الثلاثي الأبعاد في الفضاء الى ” ثمان مناطق ” و هى تكون شبيهة بمناطق النظام الثنائي الابعاد .
نظام الإحداثيات فى الفيزياء
إن ما سبق فإنه ينطبق على نظام الإحداثيات الديكارتية في الرياضيات ؛ حيث انه من العادي أن لا يتم استعمال اي وحدة للقياس ؛ و لكنه يكون من الضروري أن نقوم بتاكيد ان الابعاد فى الفيزياء هى ببساطة ” قيس لشئ ما ” ؛ أو يكون من الضروري القيام بإضافة بعد اخر ؛ و ان الاشياء متعددة الأبعاد من الممكن ان نقوم بحسابها و التحكم فيها .
ابرز الانظمة الاحداثية و نظام الإحداثيات القطبية
نظام الإحداثيات الديكارتية
يتم استخدام نظام الإحداثيات الديكارتية في الرياضيات لتحديد موقع نقطة على مستوى معين من خلال رقمين يطلق عليهم فى الغالب الاحداثية ” س ” و الاحداثية ” ص ” ؛ و فى نظام المصطلحات المغربي فإنه يعرف باسم ” مستقيم مدرج ” و الاحداثيات تعرف بالتفاصيل و التراتيب ” .
من اجل ان تقوم بتعريف الاحداثيات فإننا نقوم باسقاط خطين عموديين ” الافاضل او محور السينات ” و ” التراتيب او محور الصادات ” و من الواجب تعريف وحدة الطول أو التدريج .
من خلال نظام الإحداثيات الديكارتية من الممكن التعبير عن الأشكال الهندسية من خلال استخدام المعادلات الجبرية ؛ و تكون هذه المعادلات توافق احداثيات النقاط التى تمثل الشكل الهندسي بالفعل فمثلا ” دائرة لها شعاع مساو 2 من الممكن التعبير عنها بالمعادلة س تربيع + ص تربيع = 4 ” .
قد تم تسمية النظام الديكارتى بهذا الاسم نسبة إلى عالم الرياضيات والفيلسوف الفرنسي ” رينيه ديكارت ” والذي قد عمل جاهدا على القيام بالدمج بين الجبر و الهندسة الاقليدية و عمله كان له فوائد كثيرة فى مجال دراسة الخرائط و الدول و فى مجال الهندسة التحليلية .
ان النظام الديكارتى قد تم تطويره فى عام 1637 م فى كتابتين مختلفتين ؛ ففى الجزء الثانى من حديث الطريقة يتم القيام باستخدام محورين متقاطعين كأداة للقياس في القيام بتحديد موقع شكل أو نقطة فى المستوى .
نظام الإحداثيات الاهليجي
إن نظام الإحداثيات الاهليجي هو عبارة عن نظام إحداثيات متعامد ثنائي الأبعاد يكون فيه خطوط الإحداثيات اهليجية و متحدة فى البؤر و القطع الزائدة .
نظام الإحداثيات الاسطوانية
إن نظام الإحداثيات الاسطوانية هو عبارة عن نظام إحداثي ثلاثي الابعاد تكون فيه نقاط الفراغ معرفة بأحداث قطبيين للقيام وإسقاطاتها المتوازية على بعض المستويات الثابتة و المسافة تكون محددة الاشارة و من تلك المستويات و الاحداثيات القطبية الاولى تعرف باسم ” المسافة نصف القطرية او نصف القطر ” .
الإحداثيات القطبية الثانية تعرف باسم الموضع الزاوي أو ” زاوية السمت ” ؛ اما بالنسبة للاحداثيات القطبية الثالثة فإنها ” الارتفاع بالطبع إذا كان المستوى المرجعي افقي ” ؛ اما الخط العمودي المار على المستوى المرجعي فإنه يعرف ب ” المحور الطولي ” أو ” المحور الاسطواني ” و أن هذا الخط يمر من مركز الإحداثيات .
ان الاحداثيات الاسطوانية تكون فى غاية الاهمية و من الممكن الاستفادة منها بشكل كبير عندما ترتبط بالاجسام أو الظواهر ذات التناظر الدوراني حول محور طولي مثل ” التوزيع الحراري الموجود فى المعادن الاسطوانية ” بالاضافة الى جريان الماء في داخل أنبوب مستقيم ذو مقطع عرضي مستدير .
نظام الإحداثيات الكروية
إن نظام الإحداثيات الكروية هو عبارة عن نظام إحداثي الفضاء ثلاثي الأبعاد و فيه يتم تحديد موقع النقطة من خلال 3 أعداد و هى ( زاوية الارتقاء أو زاوية الارتفاع للنقطة من المستوى الثابت مرورا بنقطة الاصل ) ؛ ( المسافة الاشعاعية ؛ و التي تقاس من نقطة ثابتة تعرف بنقطة الأصل ) ؛ ( زاوية السمت ؛ و هى التى تقع بين الإسقاط الموازي للخط الذي يصل بين نقطة و نقطة الأصل على مستوى ثابت و بين اتجاه ثابت فى نفس المستوى ) .
انواع الاحداثيات القطبية
يوجد العديد من الاحداثيات القطبية و التى تتمثل فى الاحداثيات الكروية ؛ الدائرية و الاسطوانية .
الإحداثيات الاسطوانية
و هى احدث الاحداثيات القطبية و هى احد الانظمة الثلاثية الأبعاد ؛ حيث يتم تمثيل نقطة ” ما ” في هذا النظام الاحداثي الاسطوانية إلى ثلاثة رموز تتمثل فى ( ع ؛ غ ؛ ف ) و هى التى تقوم بالرمز الى بعض المصطلحات الديكارتية و التى تعنى نصف القطر ” و هو عبارة عن المسافة بين محور الصادات و النقطة م ” .
كما نجد أن الصمت هو عبارة عن ” الزاوية التي تقع بين المحور والنقطة م وذلك على مستوى س ص ؛ اما بالنسبة الى الرمز ف فهو الارتفاع ؛ حيث ان المسافة تكون ذات اشارة سالبة و توجد بين المستوى س ص و النقطة م .
الإحداثيات الكروية
و هو عبارة عن نظام الإحداثيات القطبية ثلاثي الأبعاد يتكون من ” نصف القطر ؛ الصادات ؛ السمت ؛ الاوج ” .
الإحداثيات الدائرية
و هو نظام احداثي قطبي ثلاثي الابعاد يعبر عن النقطة م من خلال ” ن ؛ ت ؛ ل ” .
تحويل الاحداثيات الكروية الى احداثيات خطية ثلاثية
من الممكن القيام بتحويل الاحداثيات الكروية الى الاحداثيات الخطية الثلاثية من خلال عمليات رياضية بسيطة و سهلة ؛ فان بعض المسائل فى الطبيعة يسهل القيام بحلها عند استعمال الاحداثيات الخطية ؛ و ان بعض المسائل يكون من السهل حلها عندما تستخدم الاحداثيات الكروية مثل ” انتشار الاشعة حول المصباح ” ؛ ” انتشار الاشعة حول الشمس ” .
كما ان الدوامات فى المياه يتم اعتبارها حالة خاصة من الاحداثيات الكروية و تسمى ب ” الاحداثيات الدائرية ” و هى تعمل عندما يتم معرفة ” نصف القطر ؛ و زاوية واحدة ” ؛ و من الامثلة الواضحة ( اننا نستخدم فى حياتنا اليومية للقيام بتحديد موقع مدينة ما على سطح الكرة الأرضية ” خط الطول ؛ خط العرض ” اى يحتاج إلى مقياسين الزمان لذلك ؛ و ان هذا يكون صحيح طالما ان نصف القطر للكرة الارضية يكون ثابت .
خاتمة قصيرة عن الاحداثيات القطبية
إن نظام الاحداث القطبى هو عبارة عن مجموعة من المتغيرات من خلالها يمكننا ان نعرف مكان نقطة ما في الفضاء الثلاثي الأبعاد .