بحث عن مقدمة في المتجهات
بحث عن المتجهات في الفضاء الثلاثي الابعاد فالمتجهات من أهم موضوعات علم الرياضيات التي تمكننا من فهم الكثير من العلاقات الرياضية المعقدة ، و في هذا البحث سوف نتحدث عن تعريف المتجهات و عن مركبات المتجهات و عن خصائص المتجهات و مميزات المتجهات ، كما أننا سوف نعرض العلاقات الرياضية بين المتجهات مثل جمع الكميات المتجهة و ضرب المتجهات و تساوي المتجهات و قسمة المتجهات و تاريخ المتجهات ،كما اننا سوف نعرض طريقة تمثيل الكميات المتجهة و طريقة تمثيل الكميات المتجهة من خلال التمثيل الرياضي .
تعريف المتجهات
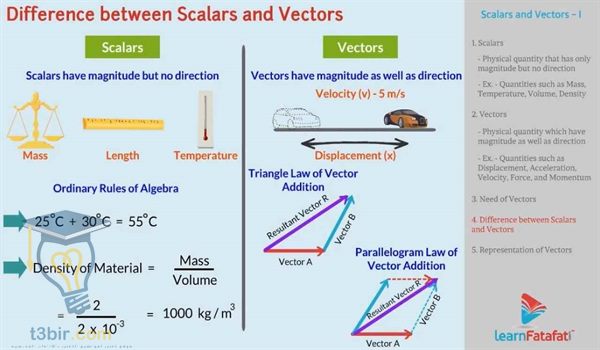
المتجهات هى الشيء المطلوب لعملية نقل النقطة ” أ ” إلى النقطة ” ب ” ، و تم استخدام مصطلح المتجهات لأول مرة من خلال علماء الفلك في القرن الثامن عشر و الذين كانوا يبحثون في دراسة الكواكب و الشمس ، إن حجم المتجهات يشير إلى المسافة بين نقطتين و يشير كذلك إلى اتجاه النقل من النقطة ” أ ” إلى النقطة ” ب ” .
جميع العمليات الجبرية الرياضية التي يتم عملها على الأعداد الحقيقية مثل الطرح و الجمع و الضرب يكون لها نظائر قريبة من المتجهات أو النواقل ، و المفهوم الأكثر شمولية للمتجهات أو النواقل هو أنها عدد من عناصر المساحة الناقلة ، و تفيدنا المتجهات كثيرا في الكثير من الدراسات العلمية حيث أنه لا يكفي قياس قوة معينة بل يجب معرفة مقدار هذه القوة و اتجاهها كذلك .
*اقرا ايضا بحث عن البوليمرات واستخدامها
مركبات المتجهات
و عند دراسة متجه معين نجد ان لكل متجه مركبات تتنوع أو تختلف بحسب نظام الإحداثيات الذي نحن فيه ، و يمكننا التعبير عن المتجهات أو تمثيلها في النظام الإحداثي الديكارتي من خلال المركبات السينية والصادية و العينية ، حيث أن المتجه يساوي هذه المركبات الثلاثة مجموعة معا ، حيث ان المركب السيني مضروب في متجه الوحدة السيني و المركب الصادي مضروب في متجه الوحدة الصادي و المركب العيني مضروب في متجه الوحدة العيني.
و المركب هو ما نعبر من خلاله عن طول المتجهات على نظام الإحداثيات الذي نقوم باستخدامه ، حيث يمكننا ان نقول ان طول المتجه على المحور السيني يساوي المركب السيني لهذا المتجه و الأمر نفسه مع المركب الصادي و المركب العيني كذلك .
خصائص المتجهات
للمتجهات الكثير من الخصائص التي تميزها عن الكميات الأخرى حيث أن خصائص الكميات المتجهة تكون أكثر من خصائص الكميات القياسية و ذلك بسبب أن الكميات المتجهة تتطلب مقدار و اتجاه حتى يمكن التعبير عنها ، و من خصائص المتجهات أنه في بعض الأحيان يتم استخدام الأسهم من أجل التعبير عنها و يعتبر طول السهم المستخدم عن مقدار المتجه الذي يعبر عنه بينما يشير اتجاه السهم إلى اتجاه هذا المتجه ، ومن أهم خصائص المتجهات هى الجمع و التساوي و الطرح و الضرب .
ويمكنك تحميل من هنا بحث عن المتجهات في الرياضيات doc جاهز للطباعه .
تساوي المتجهات
و إذا وجد متجهان لهما نفس الطول و المقدار و يكون متجهين إلى نفس الاتجاه أي يشيران إلى اتجاه واحد فإن هذان المتجهان يكونون في هذه الحالة متساويين ، و مثالا على تساوي المتجهات يمكننا القول أن هناك متجهين يشيران إلى الجنوب و مقدار كل متجه منهما 5 إذن يمكننا القول إن هذان المتجهان متساويان ، أما لو كان لأحد المتجهات مقدار مختلف عن الآخر أو انه يشير إلى اتجاه مختلف عن الآخر فإن هذين المتجهين لن يكونا متساويين .
جمع المتجهات
تقبل المتجهات الجمع و يمكننا جمع المتجهات من خلال جمع مركبات المتجه مع بعضها البعض ، حيث نقوم بجمع المركب السيني و المركب الصادي و المركب العيني مع بعضها كل على حدة ، كما انه يوجد طريقة هندسية أيضا لجمع المتجهات و ذلك من خلال تمثيل المتجه الأول ثم نقوم بوضع ذيل المتجه الثاني على رأس المتجه الأول و هكذا و في النهاية نقوم برسم سهم من ذيل المتجه الأول إلى رأس المتجه الثاني ، و هذا المتجه الأخير الذي قمنا برسمه هو حاصل عملية الجمع ويسمى المتجه المحصل ، و يتميز جمع المتجهات بخصائص الجمع التبديلية و الترابطية .
طرح المتجهات
و المتجهات تقبل الطرح كذلك ، و كما فعلنا في عملية جمع المتجهات يمكننا العمل في الطرح ، و لكن مع ملاحظة انه عملية الطرح هى نفسها عملية الجمع و لكن لن نقوم بعملية جمع متجهين كما فعلنا في عملية جمع المتجهات و لكن في عملية الطرح سوف نقوم بإضافة المتجه الأول إلى سالب المتجه الثاني ، أي أننا نقوم بإضافة المتجه الثاني و لكن بعدما نقوم بعكس اتجاه هذا المتجه .
ضرب المتجهات
المتجهات كميات تقبل الضرب كذلك ، حيث يمكننا ان نقوم بضرب متجه ما بكمية قياسية ، و عملية ضرب متجه بكمية قياسية هي عبارة عن تغيير في طول المتجه أي أننا في عملية الضرب نقوم بتغيير مقدار المتجه و لكن اتجاهه لن يتغير لو تم ضربه في أي رقم.
و اما عن ضرب المتجهات في بعضها البعض فإنه يوجد نوعين من ضرب المتجهات حيث أنه لو قمنا بضرب متجهين من خلال الضرب النقطي فإن الناتج من هذه العملية سوف يكون عبارة عن كمية قياسية و لذلك فإن هذا النوع من الضرب يعرف الضرب القياسي ، أما النوع الثاني من ضرب المتجهات فإنه يسمى الضرب الاتجاهي و فيه تقوم بضرب المتجهين ضربا تقاطعوا والناتج هنا يكون متجها جديد عمودي على المتجهين الذين قمنا بضربهما .
المتجه السالب
لو كان عندنا المتجه ” أ ” فإن المتجه السالب من هذا المتجه هو المتجه الذي يكون ناتج جمعه مع المتجه ” أ ” صفر ، فلو قمنا بجمع متجه ما مع متجه آخر ووجدنا أن ناتج هذه العملية هو صفر فإن هذا المتجه هو المتجه السالب للمتجه الذي قمنا بجمعه معه ، و المتجه السالب يكون له نفس مقدار مثيله الموجب و لكن ف اتجاه معاكس له حيث يكون الفرق بينهما 180 درجة .
متجه الوحدة
و يمكننا تعريف متجه الوحدة على أنه متجه يبلغ مقداره واحد و يكون عديم الأبعاد ، و أما عن اتجاه متجه الوحدة فإنه يعبر عن اتجاه كل مركب في مركبات المتجه ، و يختلف متجه الوحدة بحسب اختلاف النظام الاحداثي الذي نقوم باستخدامه ، حيث انه لو كانت هناك زاوية وجوده بين المحور السيني و المتجه فإن مقدار المركب السيني يكون متساوي مع طول هذا المتجه و يكون مضروب في جيب تمام هذه الزاوية ، كما أن المركب الصادي سوف يكون متساوي مع طول هذا المتجه و مضروب في جيب تمام هذه الزاوية .
أهمية المتجهات
للمتجهات الكثير من الفوائد و لها أهمية كبيرة للغاية و لا يمكن الاستغناء عنها في الكثير من العوم نظرا لأنها تساعد كثيرا في الكثير من عمليات القياس المختلفة ، وتكمن أهمية المتجهات في أنها يمكن استخدامها في قياس الكثير من الأشياء ، كما أنه يتم استخدام المتجهات في قياس سرعة السيارات و الحافلات ، و من خلال المتجهات نقوم بقياس سرعة الرياح و اتجاهها كذلك ، كما أن المتجهات يمكن من خلالها ان نقوم بقياس كثافة مادة ما ، كما أننا نستطيع استخدام المتجهات في قياس طول مكان ما و تحديد اتجاهاته كذلك .
مميزات المتجهات
و هناك الكثير من المميزات التي تميز بها المتجهات و تجعل منها هامة للغاية ، حيث أن المتجهات توفر لنا إمكانية قياس و معرفة الجهات الموجودة في أي مبنى أو عقار مختلف ، كما أن المتجهات تساعد على معرفة الفروق الموجودة بين الكميات المتجهة و بين الكميات السليمة و تمنحنا القدرة على التمييز بين هذه الكميات المختلفة .
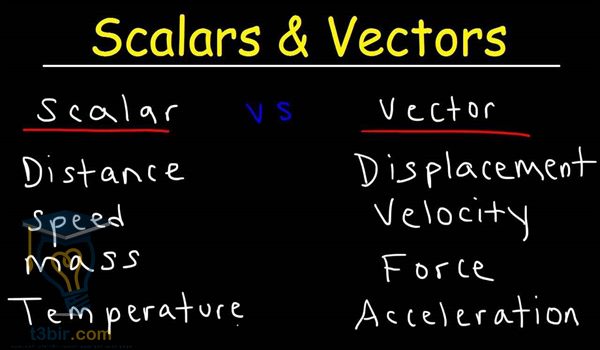
كما أنه من خلال المتجهات يمكننا تصنيف الكميات الفيزيائية المختلفة إلى كميات عددية و كميات متجهة ، من الممكن تمثيل المتجهات المختلفة من خلال الرسم ، يتم تحليل المتجهات من خلال عدة مستويات تضم محورين يقعان متعامدين و من خلالهما نحصل على قيمة كل متجه و نتعرف من خلالها على المركبات الصادية و السينية و العينية .
تاريخ المتجهات
مر مفهوم المتجهات بمراحل كثيرة من التطور حتى نراه بشكله المعاصر ، و على مدار 200 عام قدم العديد من العلماء الكثير من المساهمات في تطوير مفهوم المتجهات ، حيث قام ” Giusto Bellavita ” بتجريد و توضيح الفكرة الرئيسية الأطروحة في عام 1935 عندما قام بتأسيس مفهوم ” equipollence ” ، و قام العالم ويليام روان هاميلتون فيما بعد بتقديم مصطلح المتجهات ، و قام العديد من العلماء على رأسهم هيرمان جراسمان و كونت دي سان و أوغسطين كوشي و ماثيو أوبراين و أغسطس موبيوس بتطوير عدة انظمة مشابهة للنواقل في منتصف القرن التاسع عشر.
حيث قام جروسمان في عام 1840 بوضع نظرية الانحراف و التي تعد أول الانظمة التحليلية المكانية التي تشابه نظام اليوم ، و في عام 1878 قام ويليام كينجدون كليفورد بنشر عناصر ديناميكية و قام بتبسيط بعض الدراسات التي سبقته ، و قام إدوين بيدويل ويلسون في عام 1901 بنشر تحليل المتجهات و الذي تمت له عملية تعديل من محاضرات جيب و التي قامت بنفي أي ذكر لقضية التأخر في عملية تطوير المتجهات في حساب التفاضل و التكامل .