بحث عن متوازي الاضلاع اولى ثانوي

ما هو متوازى الاضلاع ؟

بحث عن متوازى الاضلاع وحالاته الخاصة حيث أن متوازي الاضلاع هو احد الاشكال الهندسية الرباعية الاضلاع ؛ حيث ان متوازى الاضلاع يتميز بان له اربع اضلاع و كل ضلعين متقابلين يكونان متطابقان و متوازيان معا أو يكونا متطابقين فقط او متوازيان فقط ؛ كما أن متوازى الاضلاع له أربع زوايا و مجموع زواياه يصل الى 360 درجة مثل اى شكل رباعى .

ان قياس كل زاويتان متقابلتان فى متوازى الاضلاع يكون متساوى ؛ و يحتوى متوازي الاضلاع على قطرات يتقاطع كل منهما مع الآخر في منتصف الشكل و ينصف كل منهما الآخر حيث أن كل قطر يصل الى بين الزاويتان المتقابلتان ؛ و من الخصائص لمتوازى الاضلاع ان كل زاويتان على ضلع واحد يكون مجموعهما 180 درجة ؛ و قد يطلق على متوازي الاضلاع اسم آخر و هو ” شبيه المعين ” .

محيط متوازي الاضلاع

ان محيط اى شكل هندسي هو ( مجموع اطوال اضلاعه ) و يتم قياس المحيط وحدة الأطوال و ان محيط متوازي الاضلاع = مجموع أطوال أضلاعه .

مثال : –

متوازي أضلاع طول أحد أضلاعه 4 سم و الضلع الآخر طوله 5 سم قم بحساب محيطه ؟

الحل

مما يتضح من المعطيات وأبعاد هذا الشكل فإنه من النوع الذي يكون فيه كل ضلعين متقابلين يكون لهما نفس الطول و بالتالى فإن أطوال الاضلاع للشكل على التوالى هى ( 5 ؛ 4 ؛ 5 ؛ 4 سم ) .

محيط متوازي الاضلاع = مجموع أطوال أضلاعه

محيط متوازي الاضلاع = 4 + 5 + 4 + 5 = 14 سم .
*اقرا ايضا : بحث عن حرف ومهن الانبياء قصير ملخص

مساحة متوازى الاضلاع

أن متوازى الاضلاع يعد من الاشكال الثنائية الابعاد فيتم رسم في المستوى الديكارتي على محاورين و هما ” المحور السينى ؛ المحور الصادى ” و أن لكل شكل ثنائي الأبعاد مساحة وقد تم اشتقاق مساحة متوازى الأضلاع من مساحة كل من ” المثلث و المستطيل ” .

أن متوازي الأضلاع لو تم تجزئته إلى جزأين فسوف تجدهم المستطيل والمثلث في استنتج علماء الرياضيات القانون التالى ( مساحة متوازى المستطيلات = طول القاعدة × طول الارتفاع الساقط على القاعدة ) .

مثال : –

متوازي أضلاع طول أحد الأضلاع الموجودة فيه 4 سم ؛ و طول الضلع الآخر هو 5.5 سم فقم بحساب مساحة متوازى الأضلاع ؟

الحل

فى البداية سوف تحتاج إلى رسم شكل متوازى الاضلاع على الورق بالابعاد المعطاة بالاعلى .

بعد ذلك قم بإسقاط عمود من طرف الزاوية العليا للشغل على الخط الأفقي وهو يمثل ” قاعدة الشكل ” .

عن طريق استخدام المسطرة قم بقياس طول هذا الارتفاع و فى هذا المثال سوف تساوى 3 سم .

من خلال تطبيق قانون مساحة متوازى الأضلاع = طول القاعدة × الارتفاع

مساحة متوازى الأضلاع = 4 × 3 = 12 سم مربع .

ارتفاع متوازي الأضلاع

ما يقصد بارتفاع متوازي الأضلاع هو طول العمود الذي يسقط من أحد رأسه على الضلع المقابل أو على امتداده .

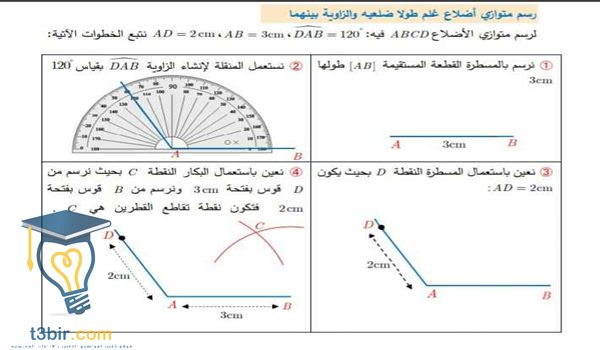
كيفية رسم متوازي الاضلاع ؟

لكى تقوم برسم متوازى الاضلاع من خلال معرفة طول ضلعيه المتجاورين و كذلك معرفة قياس زاوية نقوم باتباع الخطوات التالية:-

قم برسم قطعة مستقيمة بقياس احد الاضلاع و لنفترض انه 4 سم ؛ بعد ذلك قم بوضع المنقلة حيث تكون نقطة المنتصف على أحد طرفي القطعة التى تم رسمها و قم بتحديد قياس الزاوية و لتكن مثلا 70 درجة .

قم بالتوصيل بين طرف القطعة المستقيمة و مكان تحديد قياس الزاوية بالطول الآخر للضلع الآخر وليكن 5 سم ؛ و بعد ذلك قم بوضع الفرجار عند الطرف الحر للقطعة المستقيمة و التى يصل طولها الى 5 سم ثم قم بفتح الفرجار بطول 4 سم و قم برسم قوس .

قم بوضع الفرجار عند الطرف الآخر و الحر للقطعة المستقيمة و التى يصل طولها الى 4 سم و افتح الفرجار بطول 5 سم و قم برسم القوس حتى يتقاطع مع القوس الاول فى نقطة .

قم بتوصيل نقطة تقاطع القوسين مع كل من الطرفين البحرين القطعتين المستقيمتين من خلال استخدام المسطرة و عند القيام بقفل هذا الشكل فانك سوف تحصل على متوازي الأضلاع .

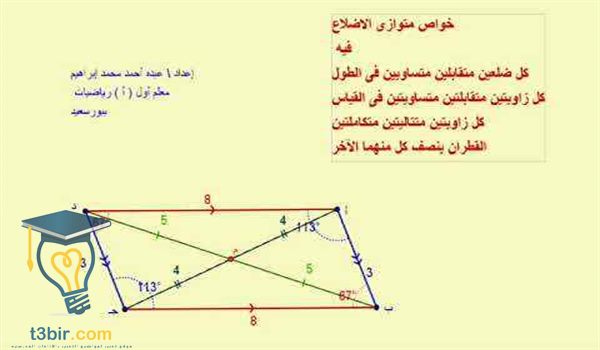
خصائص متوازي الأضلاع

ان كل ضلعين متقابلين فى متوازى الاضلاع يكونان متساويين .

ان كل ضلعين متقابلين في متوازي الأضلاع يكونان متوازيين .

ان كل قطر موجود فى متوازى الأضلاع يكون نصف القطر الآخر .

ان مساحة متوازى الأضلاع = ضعف مساحة المثلث الذي يتشكل من ضلعين و قطر .

ان قطري متوازي الأضلاع يتقاطعان في نقطة تشكل ” مركز التناظر لمتوازى الاضلاع ” و تسمى ب ( مركز متوازي الأضلاع ) .

كل زاويتين متقابلتين في متوازي الأضلاع يكونا متساويتان .

إن مجموع مربعات أطوال الأضلاع = مجموع مربعي طولي القطريين ” و هذا هو قانون متوازي الأضلاع ” .

إن مجموع كل زاويتين متحالفتين على ضلع واحد من أضلاع متوازي الأضلاع تكون 180 درجة .

أن تحقق واحد فقط من الخصائص السابقة فى المضلع الرباعي المحدب يعني أن هذا الشكل ” متوازي اضلاع ” ؛ بالاضافة الى ان اثبات ان ضلعين متقابلين و متوازيين و متقايسين في آن معا يقوم بإثبات أن هذا الشكل متوازي اضلاع .

شروط يجب ان تكون متوفرة لكي يكون الشكل الهندسي متوازي اضلاع

ان تطابق اى ضلعان متقابلان فى اى شكل هندسى فان هذا الشكل يكون متوازي اضلاع .

عندما يتقابل أو يتوازى او يتقابل اى ضلعين داخل أي شكل رباعي هندسي فانه يتحول الى متوازي اضلاع .

ان كانت الأقطار الموجودة داخل الشكل تقوم بتنظيف بعضها البعض فإن هذا الشكل يتحول إلى متوازي اضلاع .

فى حالة ان تساوت الزوايا التى تكون مقابلة لبعضها فإن هذا الشكل يتحول الى متوازي اضلاع .

ان كانت نتيجة قياس اى زاويتان متقابلتان 180 درجة فإن هذا الشكل يكون متوازي اضلاع .

حالات خاصة لمتوازي الأضلاع

أن متوازى الاضلاع له الكثير من الاستثناءات من حيث أن بعض الحالات مثل أن تكون جميع الأقطار متعامدة أو أن تتساوى الاضلاع و فى تلك الحالات من الممكن ان يكون الشكل معين .

فى بعض الاحيان من الممكن ان يكون متوازي الأضلاع مستطيلا عندما تتساوى الأقطار او عند وجود احد زوايا الشكل تكون زاوية قائمة و تساوي 90 درجة .

و من الممكن ان يكون هناك وجود للشكلين معا كل من المستطيل والمعين فيتحول هذا الشكل إلى الشكل الهندسي المربع .

و أن هذه الحالات الخاصة والاستثنائية للقيام بتحويل متوازى الاضلاع الى عدد من الأشكال الهندسية الاخرى ؛ و ان متوازى الاضلاع من الأشكال الهندسية المهمة و التى يقوم المهندسين باستخدامها في الكثير من الأمور الهندسية و فى التصميمات وغيرها من الاستخدامات .

بعض الاشكال الرباعية الأخرى

يوجد عدة اشكال رباعية اخرى تكون نوعا من ضمن انواع متوازى الاضلاع و تكون مختلفة و هى كالاتى : –

المعين

ان المعين يختلف عن متوازى الاضلاع فى ان جميع اضلاعه تكون متساوية كما ان أقطاره تكون متعامدة وكل منهما يقوم بتنظيف القطر الآخر كما يقوم بتنظيف زاوية الرأس ؛ ويكون قياسا زاويتين متتاليتين فيه يساوي 180 درجة و أطفاله الأربعة تتساوى فى القياس .

المربع

ان المربع يعد نوع من انواع متوازى الاضلاع و لكنه يختلف عنه فى ان جميع الزوايا الموجودة داخل المربع تكون زوايا قائمة اى تساوي 90 درجة ؛ و أن أضلاع المربع تكون متطابقة و متساوية فى الاطوال و أقطاره تكون متعامدة و متناصفة و متطابقة ؛ و يكون محيط المربع هو أربعة أضعاف طول ضلع واحد منه.

المستطيل

ان المستطيل شكل من ضمن اشكال متوازى الاضلاع و لكن يكون اختلافه عنه في أن جميع زواياه تكون قائمة كما أن الأقطار تكون متطابقة و متناصفة و محيطه يكون ضعف المجموع الكلى لكل من العرض و الطول .

شبه المنحرف

ان شبه المنحرف من ضمن اشكال متوازى الاضلاع ويكون له شكلان وهما ( شبه منحرف متساوي الساقين ؛ شبه منحرف به ضلعين متوازيين ) و من الممكن أن يتم تعريفه على أنه رباعي الأضلاع ويكون له فقط ضلعين متقابلين و متوازيين و بهذا فمن الممكن أن يتم استثناء متوازى الاضلاع مما يعتبره حالة خاصة لشبه المنحرف .

الدالتون

أن الدالتون هو احد انواع متوازى الاضلاع و لكنه يتكون من مثلثين متساويين الساق كما انهما يشتركان معا فى قاعدة واحدة و ما يميزه هو أن اقطاره تكون متعامدة على بعضها البعض و تكون كل زاوية جانبية مساوية للاخرى .

بعض التمارين على متوازي الأضلاع

التمرين الأول

متوازي أضلاع مساحته تبلغ 36 سم و يبلغ ارتفاعه الى 4 سم فما هو طول القاعدة المتوقع ؟

الحل

مساحة متوازى الأضلاع = طول القاعدة × الارتفاع

طول قاعدة متوازي الاضلاع = مساحة متوازي الأضلاع÷ طول الارتفاع

طول قاعدة متوازي الأضلاع = 36 ÷ 4 = 9 سم .

التمرين الثاني

متوازي أضلاع يبلغ طول قاعدته 6 سم وارتفاعه يصل الى 4 سم فما هي مساحة متوازي الأضلاع ؟ و ان كان طول الضلع المجاور 5 سم فما هو طول ارتفاعه الأكبر ؟

الحل

مساحة متوازى الأضلاع = طول القاعدة × الارتفاع

مساحة متوازى الأضلاع = 6 × 4 = 24 سم 2

الارتفاع الأكبر لمتوازى الاضلاع = مساحة متوازي الأضلاع ÷ القاعدة الصغرى

الارتفاع الأكبر = 24 ÷ 5 = 4.8 سم .

التمرين الثالث

قم بحساب محيط متوازي الاضلاع ان كان قياس أضلاعه هو 4 سم ؛ 4 سم ؛ 6 سم ؛ 6 سم .

الحل

محيط متوازي الأضلاع = مجموع أطوال أضلاع المتوازى

محيط متوازي الأضلاع = 4 + 4 + 6 + 6 = 20 سم.

خاتمة قصيرة عن متوازي الأضلاع

أن متوازي الأضلاع هو عبارة عن احد الاشكال الثنائية الابعاد و يقوم رسمه فى مستويات ديكارتية على محاور السينية و المحاور الصادية .