بحث عن المثلثات المتشابهة

مقدمة بحث عن المثلثات المتشابهة

بحث كامل عن المثلثات المتشابهة المثلثات من أهم و أشهر الأشكال الهندسية على الإطلاق ، و ذلك لأن الشكل المثلث من أقوى الأشكال الهندسية و لذلك يتم الاعتماد عليه في الكثير من الأعمال المتعلقة بالهندسة و المباني المختلفة لان الشكل الهندسي يتميز بالتحمل للكثير من الأمور و يرجع ذلك إلى أنه من الأشكال المغلقة التي تكون أضلاعه متحدة مما يمنحه قوة كبيرة .

وقد اهتم علماء الرياضيات والهندسة بالمثلثات بشكل كبير و قاموا بوضع القوانين الخاصة بها فيما يعرف بحساب المثلثات كما قدم العديد من العلماء عدة نظريات تتعلق زوايا المثلث و تم الاستفادة منها في العديد من التطبيقات الهندسية ، و في هذا البحث سوف نعرض أحد الأمور الهامة المتعلقة بالمثلثات و هى المثلثات المتشابهة حيث أننا سوف نقوم بعرض تعريف المثلثات و تعريف المثلثات المتشابهة و حالات تشابه المثلثات و النتائج المترتبة على تشابه المثلثات و أهمية علم المثلثات و غيرها العديد من العناصر المهمة التي تتعلق المثلثات المتشابهة .

تعريف المثلثات

قبل أن نشرع في الحديث عن المثلثات المتشابهة يجب أن نعرف في البداية ما هى المثلثات و يجب ان نتعرف على التعريف الواضح للمثلثات حتى يسهل علينا التعرف على باقي المواضيع المتعلقة بها .

و المثلثات هى أحد الأشكال الرئيسية في علم الرياضيات تتكون من عدة قطع مستقيمة تصل بين ثلاث نقاط تسمى هذه القطع المستقيمة بأضلاع المثلث و تسمى النقاط التي تصل بينها برؤوس المثلث ، و المثلثات من الأشكال ثنائية الأبعاد و هى أشكال مغلقة تتكون من ثلاث زوايا و ثلاثة أضلاع ، و من شروط المثلثات أن يكون مجموع طولي أي ضلعين فيها أكبر من طول الضلع الثالث ، تم وضع العديد من القوانين المختلفة للمثلثات مثل القوانين الخاصة بمحيط المثلثات و مساحتها و العديد من النظريات مثل نظرية فيثاغورس .
*اقرا ايضا بحث عن المعين والمربع في الرياضيات 

تعريف المثلثات المتشابهة

بعدما تعرفنا على تعريف المثلثات سوف نقوم بتوضيح تعرف المثلثات المتشابهة و معنى هذا المصطلح ، حيث يشير مصطلح المثلثات المتشابهة إلى واحدة من العلاقات الرياضية المختلفة التي قد تحدث بين مثلثين ، و تقوم علاقة تشابه المثلثات على علاقة نسبية أي أنها تعتمد على النسبة و التناسب بين المثلثين.

حيث أنه يحدث في علاقة تشابه المثلثات أن تكون جميع زوايا المثلث بنفس القياس و لكن تكون أطوال أضلاع المثلثين مختلفة بنسبة تكون هى نفس النسبة بين كل ضلعين متقابلين .

حالات تشابه المثلثات

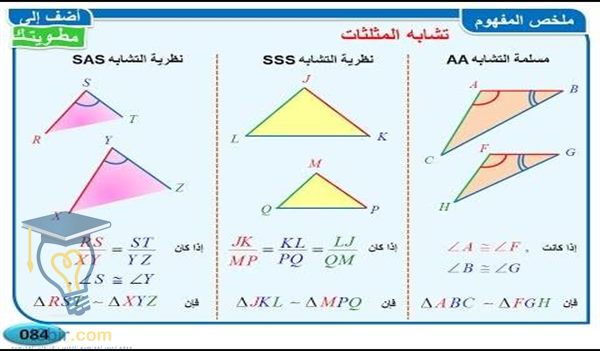
و هناك عدة حالات تحدث فيها علاقة تشابه المثلثات حيث أنه توجد حالات هامة حتى نستطيع من خلالها معرفة تشابه المثلثات أو أنها غير متشابهة ، الحالة الأولى هي تشابه الأضلاع وهي التي يحدث فيها تشابه بين جميع أضلاع المثلثين الثلاثة حيث يحدث تناسب بين كل ضلعين يكونوا في حالة تقابل فعلى سبيل المثال لو كان لدينا مثلثين الأول تكون أضلاعه أ و ب و ج و المثلث الثاني تكن أضلاعه س و ص و ع و لاحظنا أن أ ب / س ص = ب ج / ص ع = ج أ / ع س في هذه الحالة يكون المثلث أ ب ج متشابه مع المثلث س ص ع لتوافر التشابه بين جميع أضلاعه .

الحالة الثانية تشابه المثلثات هي تشابه زاويتين من زوايا المثلثين و مثالا على ذلك لو كان لدينا مثلثين الأول المثلث أ ب ج و الثاني المثلث س ص ع فلو لاحظنا الزاوية ب تتشابه مع الزاوية المقابلة لها في المثلث الثاني و هى ص و كانت الزاوية ج من المثلث الأول تتساوى مع الزاوية التي تقابلها من المثلث الثاني و هى الزاوية ع فإن المثلثين في هذه الحالة يكونوا متشابهين.

و أما الحالة الثالثة تشابه المثلثات فهي تشابه ضلعين و زاوية فلو كان الضلعين المتقابلين في المثلثين متشابهين مع توافر تساوي الزاوية الواقعة بين الضلعين في كلا المثلثين و مثالا على ذلك لو كان لدينا مثلثين الأول المثلث أ ب ج و الثاني المثلث س ص ع فلو لاحظنا تشابه بين الأضلاع أ ب / س ص = يب ج / ص ع مع وجود تشابه بين الزاوية أ ب ج و بين الزاوية س ص ع فإن المثلثين في هذه الحالة يكونوا متشابهين .

النتائج المترتبة على تشابه المثلثات

هناك العديد من النتائج المترتبة على العلاقة الرياضية التي تحدث من خلال تشابه المثلثات و التي يستفيد منها العلماء في الكثير من التطبيقات العملية و الكثير من التصاميم الهندسية ، و يترتب على حالات تشابه المثلثات التي قمنا بذكرها أن يكون هناك تساوي بين النسبة بين محيط كلا المثلثين المتشابهين مع النسبة بين طول أي ضلعين يكونوا متقابلين في المثلثين ، كما يترتب على تشابه المثلثات أيضا وجود تشابه بين النسبة بين مساحة المثلثين المتشابهين مع النسبة بين طولي أي ضلعين متقابلين في المثلثين .

قوانين المثلثات

و هناك عدة قوانين خاصة بحساب المثلثات و الحصول على التفاصيل الخاصة بكل مثلث مثل الحصول على القياس الخاص بمحيط المثلث أو مساحته أو أطوال أضلاعه ، و ينص قانون مساحة المثلث على أنه تساوي مساحة أي مثلث حاصل ضرب طول نصف قاعدته في ارتفاعه و المقصود بالارتفاع هنا هو العمود الساقط من أحد زوايا المثلث على الضلع المقابل لها و الذي يطلق عليه اسم القاعدة بحيث يصنع هذا العامود زاوية قائمة مع القاعدة و بهذا تساوي مساحة المثلث ½ القاعدة x الارتفاع.

و اما عن القانون الخاص بمحيط المثلث فإنه ينص على أن محيط المثلث يساوي مجموع أطوال أضلاع المثلث و لكن بشرط أن تكون وحدات القياس متساوية و بهذا يساوي محيط المثلث طول الضلع الأول + طول الضلع الثاني = طول الضلع الثالث .

الاستخدامات العملية قوانين المثلثات

و كما ذكرنا ان القوانين و النظريات الخاصة بعلم المثلثات هام للغاية لأنه يتم استخدامها في الكثير من التطبيقات العملية ، و من أهم الاستخدامات العملية قوانين المثلثات هي حساب وقياس الارتفاعات المختلفة حيث أنه من خلال تطبيق القوانين الخاصة بالمثلثات مثل قوانين أو حالات تشابه المثلثات تمكننا من حساب ارتفاع نقطة معينة دون الحاجة لقياسها بشكل فعلي .

كما أن هذه القوانين هامة في مجال الألعاب الالكترونية و التصاميم الخاصة بهذه الألعاب حيث أنها هى ما تمنح هذه التصميمات أسلوب الحركة بشكل مائل .

كما أن المهندسين يحتاجون هذه القوانين عند القيام بأي أعمال إنشائية أو معمارية ليتمكنوا من معرفة حساب المساحات و الأبعاد و زوايا الارتفاع و زوايا البناء و معرفة مساقط الضوء ، كما تستخدم قوانين المثلثات في المسائل المتعلقة بالجرائم و التحقيقات من خلال استخدامها لمعرفة زاوية سقوط جسم ما أو معرفة زاوية أطلاق النار ، كما تستخدم قوانين المثلثات في الأمور المتعلقة بهندسة القطع البحرية مثل الغواصات .
*اقرا ايضا خاتمة عن المخدرات

أنواع المثلثات

هناك العديد من أنواع المثلثات المختلفة و التي تفيد جميعها في العديد من الاستخدامات العلمية و العملية و النظرية التي تتطلب المواصفات الخاصة التي تتميز بها هذه المثلثات ، و من أشهر أنواع المثلثات هو المثلث متساوي الأضلاع وهو المثلث التي تكون فيها أطوال الأضلاع الثلاثة متساوية و تكون قياسات الزوايا الخاصة به متساوية كذلك و يكون قياس كل زاوية من زواياه 60 درجة ، و من أشهر أنواع المثلثات أيضا المثلث المتساوي الساقين و هو المثلث الذي يكون فيه ضلعين متساويين في الطول كما أن قياس الزاويتان المقابلتان للضلعين يكونوا متساويين كذلك.

و النوع الثالث من المثلثات هو المثلث المختلف الأضلاع وهو المثلث التي تكون فيها أطوال أضلاعه مختلفة بالإضافة إلى أن قياسات الزوايا تكون مختلفة كذلك ، كما ان هناك انواع مختلفة المثلثات حسب القياسات الخاصة بالزوايا الخاصة بها حيث يتم تصنيف المثلثات حسب قياسات الزوايا إلى مثلث حاد الزوايا و هو المثلث الذي يكون فيه كل زاوية قياسها أقل من 90 درجة ، و مثلث قائم الزاوية و هو المثلث الذي يحتوي على زاوية يكون قياسها 90 درجة ، مثلث منفرج الزاوية و هو المثلث الذي يحتوي على زاوية قياسها أكبر من 90 درجة .

خاتمة قصيرة عن تشابه المثلثات

تحدثنا في بحث عن تشابه المثلثات عن العديد من النقاط الهامة المتعلقة بتشابه المثلثات حيث قمنا بعرض تعريفها و حالات تشابه المثلثات و غيرها من النقاط الهامة و في نهاية البحث نتمنى انه يكون قد لاقى اعجابكم .